
分析 (1)将所求的式子的分子、分母同时除以cos2x,化为关于正切函数的式子,把tanx=2代入可得结果.
(2)将所求的式子的分子、分母同时除以cosx,化为关于正切函数的式子,把tanx=2代入可得结果.
解答 解:(1)$\frac{2}{3}{sin^2}x+\frac{1}{4}{cos^2}x=\frac{{\frac{2}{3}{{sin}^2}x+\frac{1}{4}{{cos}^2}x}}{{{{sin}^2}x+{{cos}^2}x}}=\frac{{\frac{2}{3}{{tan}^2}x+\frac{1}{4}}}{{{{tan}^2}x+1}}=\frac{7}{12}$;
(2)$\frac{cosx+sinx}{cosx-sinx}=\frac{1+tanx}{1-tanx}=\frac{1+2}{1-2}=-3$.
点评 本题考查了同角的三角函数的关系,属于基础题.


科目:高中数学 来源: 题型:选择题
 美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( )
美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( )| A. | 2.81 | B. | 2.82 | C. | 2.83 | D. | 2.84 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
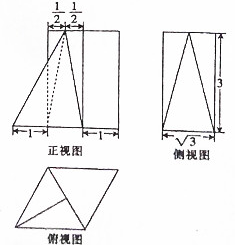
| A. | $4\sqrt{3}$ | B. | $5\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $8\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com