Question

11．P是棱长为2的正四面体内任意一点，则它到该正四面体各个面的距离之和等于$\frac{2\sqrt{6}}{3}$．

Answer 1

分析 先求出正四面体的体积，利用正四面体的体积相等，求出它到四个面的距离．

解答 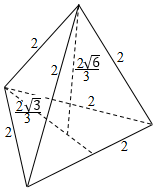解：因为正四面体的体积等于四个三棱锥的体积和，
设它到四个面的距离分别为a，b，c，d，
由于棱长为1的正四面体，故四个面的面积都是 $\frac{1}{2}$×2×2×sin60°=$\sqrt{3}$．
又顶点到底面的投影在底面的中心，此点到底面三个顶点的距离都是高的
，又高为2×sin60°=$\sqrt{3}$，
故底面中心到底面顶点的距离都是：$\frac{2\sqrt{3}}{3}$．
由此知顶点到底面的距离是 $\sqrt{{2}^{2}-（{\frac{2\sqrt{3}}{3}）}^{2}}$=$\frac{2\sqrt{6}}{3}$．
此正四面体的体积是 $\frac{1}{3}$×$\sqrt{3}$×$\frac{2\sqrt{6}}{3}$=$\frac{1}{3}$×$\sqrt{3}$×（a+b+c+d）．
所以：a+b+c+d=$\frac{2\sqrt{6}}{3}$．
故答案为：$\frac{2\sqrt{6}}{3}$．

点评 本题是中档题，考查正四面体的体积的计算，转化思想的应用，考查空间想象能力，计算能力．