
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 (1)(2)(3)利用基本不等式的性质即可判断出结论.(4)换元利用导数研究函数的单调性即可得出.
解答 解:(1)$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$=$\sqrt{{x}^{2}+1}$+$\frac{1}{\sqrt{{x}^{2}+1}}$≥2,x=0时取等号,即最小值为2,正确;
(2)x→-∞时,2-3x-$\frac{4}{x}$→+∞,无最大值,不正确;
(3)取x=$\frac{1}{2}$,logx10+lgx<0,因此最小值不为2不正确;
(4)令sin2x=t∈(0,1],sin2x+$\frac{4}{si{n}^{2}x}$=t+$\frac{4}{t}$=f(t),f′(t)=1-$\frac{4}{{t}^{2}}$<0,
因此函数f(t)在t∈(0,1]上单调递减,f(t)的最小值为f(1)=5.因此不正确.
其中真命题的个数是1.
故选:C.
点评 本题考查了基本不等式的性质、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:解答题
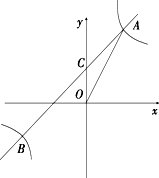 如图,反比例函数y=$\frac{2}{x}$的图象与一次函数f(x)的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.
如图,反比例函数y=$\frac{2}{x}$的图象与一次函数f(x)的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{4}{5}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c<d | B. | d<a<c<b | C. | a<c<b<d | D. | c<b<a<d |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com