
【题目】如图,在矩形ABCD中,AB=1,AD= ![]() ,P矩形内的一点,且AP=
,P矩形内的一点,且AP= ![]() ,若
,若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,(λ,μ∈R),則λ+
,(λ,μ∈R),則λ+ ![]() μ的最大值为 .
μ的最大值为 . 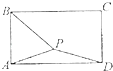
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年被业界称为![]() (虚拟现实技术)元年,未来
(虚拟现实技术)元年,未来![]() 技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某
技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某![]() 教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需
教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需![]() 团队投入15天时间,
团队投入15天时间, ![]() 团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需
团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需![]() 团队投入20天时间,
团队投入20天时间, ![]() 团队投入16天时间,总费用15万元,乙产品售价为25万元/件,
团队投入16天时间,总费用15万元,乙产品售价为25万元/件, ![]() 、
、![]() 两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() ,并且直线
,并且直线![]() 平分圆
平分圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在直线
两点,是否存在直线![]() ,使得
,使得![]() (
(![]() 为坐标原点),若存在,求出
为坐标原点),若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣lnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)﹣x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为2的等差数列,且a1 , a4 , a13成等比数列,数列{ ![]() }是首项为1,公比为3的等比数列.
}是首项为1,公比为3的等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)设数列{an+bn}的前n项和Rn , 若不等式 ![]() ≤λ3n+n+3对n∈N*恒成立,求λ的取值范围.
≤λ3n+n+3对n∈N*恒成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() 三所高校,其学生会学习部有“干事”人数分别为
三所高校,其学生会学习部有“干事”人数分别为![]() ,现采用分层抽样的方法从这些“干事”中抽取
,现采用分层抽样的方法从这些“干事”中抽取![]() 名进行“大学生学习部活动现状”调查.
名进行“大学生学习部活动现状”调查.
(1)求应从![]() 这三所高校中分别抽取的“干事”人数;
这三所高校中分别抽取的“干事”人数;
(2)若从抽取的![]() 名干事中随机选两名干事,求选出的
名干事中随机选两名干事,求选出的![]() 名干事来自同一所高校的概率.
名干事来自同一所高校的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com