
分析 通过分段函数求出a,b,c,得到a+3b+c的表达式,通过构造函数利用函数的导数求解函数的最值,推出结果即可.
解答 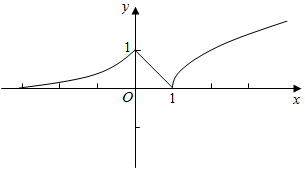 解:f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤0}\\{1-x,0<x<1}\\{\sqrt{x-1},x≥1}\end{array}\right.$,若a<b<c,f(a)=f(b)=f(c),
解:f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤0}\\{1-x,0<x<1}\\{\sqrt{x-1},x≥1}\end{array}\right.$,若a<b<c,f(a)=f(b)=f(c),
令f(a)=f(b)=f(c)=t,
可得a=lnt,b=1-t,c=t2+1,t∈(0,1).
则:a+3b+c=lnt+t2-3t+4,t∈(0,1).
令f(t)=lnt+t2-3t+4,t∈(0,1).
则f′(t)=$\frac{1}{t}$+2t-3=$\frac{(2t-1)(t-1)}{t}$,t∈(0,1).
当$\frac{(2t-1)(t-1)}{t}$=0解得t=1或t=$\frac{1}{2}$,
t∈(0,$\frac{1}{2}$)时,f′(t)>0,f(t)是增函数.t∈($\frac{1}{2}$,1)时,f′(t)<0,f(t)是减函数.
t=$\frac{1}{2}$时,函数取得最大值:$\frac{11}{4}-ln2$.
t→0时,函数f(t)趋向于-∞,无最小值.
实数a+3b+c的取值范围是:(-∞,$\frac{11}{4}-ln2$].
故答案为:(-∞,$\frac{11}{4}-ln2$].
点评 本题考查函数的导数的综合应用,数形结合,考查分析问题解决问题的能力,转化思想的应用.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (0,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,1] | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校高三年级800名学生在一次百米测试中,成绩全部介于13秒与18秒之间.抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部介于13秒与18秒之间.抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com