
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、
|
| 3 |
| 3 |
| 3 |
| c |
| 2 |
| ||
| 2 |
| c |
| 2 |
| ||
| 2 |
| ||
| a2 |
| ||
| b2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
| 1 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
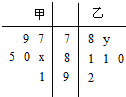 某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )
某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )| A、6 | B、7 | C、8 | D、9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
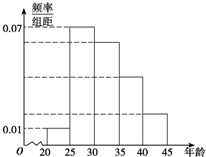 如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )
如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图,现已知年龄在[30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为( )| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 7π |
| 24 |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(1)(2) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、-2010 |
| B、-2011 |
| C、-2012 |
| D、-2013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com