
 如图AB是圆O的一条弦,过点A作圆的切线AD,作BC⊥AC,与该圆交于点D,若AC=2$\sqrt{3}$,CD=2.
如图AB是圆O的一条弦,过点A作圆的切线AD,作BC⊥AC,与该圆交于点D,若AC=2$\sqrt{3}$,CD=2.分析 (1)取BD中点为F,连结OF,求出BC,可得BF,利用勾股定理求圆O的半径;
(2)证明四边形OADB为平行四边形,利用E为AB的中点,即可证明O,E,D三点共线.
解答  (1)解:取BD中点为F,连结OF,由题意知,OF∥AC,OF=AC.
(1)解:取BD中点为F,连结OF,由题意知,OF∥AC,OF=AC.
∵AC为圆O的切线,BC为割线,
∴CA2=CD•CB,
由$AC=2\sqrt{3},CD=2$,∴BC=6,
∴BD=4,BF=2
在Rt△OBF中,由勾股定理得,$r=OB=\sqrt{O{F^2}+B{F^2}}=4$.(5分)
(2)证明:由(1)知,OA∥BD,OA=BD
∴四边形OADB为平行四边形,
又∵E为AB的中点,
∴OD与AB交于点E,
∴O,E,D三点共线.(5分)
点评 本小题主要考查平面几何的证明,具体涉及到圆的切线的性质,切割线定理等内容.本小题重点考查考生对平面几何推理能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
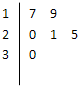 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级号x | 1 | 2 | 3 | 4 | 5 |
| 近视眼率y | 0.1 | 0.15 | 0.2 | 0.3 | 0.39 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com