
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合向量数量积的应用进行判断即可.
解答 解:若$\overrightarrow{AB}$•$\overrightarrow{AC}$<0,即|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC<0,
即-1≤cos∠BAC<0,则$\frac{π}{2}$<∠BAC≤π,则∠BAC是钝角不一定成立,
反之若∠BAC是钝角,则cos∠BAC<0,即$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC<0,
则$\overrightarrow{AB}$•$\overrightarrow{AC}$<0成立,
即p是q的必要不充分条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,利用向量数量积的定义是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
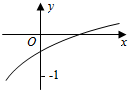 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )| A. | 0<a-1<b-1<1 | B. | 0<b-1<a<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com