
分析 根据cos(θ+$\frac{π}{4}$)求出sin(θ+$\frac{π}{4}$)、cos2θ和sin2θ,利用cosθ=cos[(θ+$\frac{π}{4}$)-$\frac{π}{4}$]和两角差的正弦值,即可求出结果.
解答 解:cos(θ+$\frac{π}{4}$)=-$\frac{\sqrt{10}}{10}$,θ∈(0,$\frac{π}{2}$),
∴sin(θ+$\frac{π}{4}$)=$\sqrt{1{-cos}^{2}(θ+\frac{π}{4})}$=$\sqrt{1{-(-\frac{\sqrt{10}}{10})}^{2}}$=$\frac{3\sqrt{10}}{10}$,
cos2θ=sin2(θ+$\frac{π}{4}$)=2sin(θ+$\frac{π}{4}$)cos(θ+$\frac{π}{4}$)=2×(-$\frac{\sqrt{10}}{10}$)×$\frac{3\sqrt{10}}{10}$=-$\frac{3}{5}$,
sin2θ=-cos(2θ+$\frac{π}{2}$)=-(2cos2(θ+$\frac{π}{4}$)-1)=-2×${(-\frac{\sqrt{10}}{10})}^{2}$+1=$\frac{4}{5}$,
∴cosθ=cos[(θ+$\frac{π}{4}$)-$\frac{π}{4}$]=cos(θ+$\frac{π}{4}$)cos$\frac{π}{4}$+sin(θ+$\frac{π}{4}$)sin$\frac{π}{4}$
=-$\frac{\sqrt{10}}{10}$×$\frac{\sqrt{2}}{2}$+$\frac{3\sqrt{10}}{10}$×$\frac{\sqrt{2}}{2}$
=$\frac{\sqrt{5}}{5}$;
sin(2θ-$\frac{π}{3}$)=sin2θcos$\frac{π}{3}$-cos2θsin$\frac{π}{3}$
=$\frac{4}{5}$×$\frac{1}{2}$-(-$\frac{3}{5}$)×$\frac{\sqrt{3}}{2}$
=$\frac{4+3\sqrt{3}}{10}$.
故答案为:$\frac{{\sqrt{5}}}{5}$,$\frac{{4+3\sqrt{3}}}{10}$.
点评 本题考查了两角和与差的三角函数求值问题,也考查了二倍角公式与同角的三角函数关系应用问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
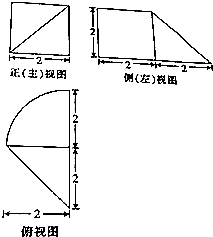
| A. | 2π+$\frac{4}{3}$ | B. | 4π+$\frac{4}{3}$ | C. | 4π+4 | D. | 2π+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
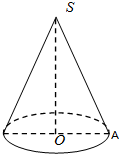 如图,课桌上放着一个圆锥SO,点A为圆锥底面圆周上一点,SA=2cm,OA=1cm,蚂蚁从点A沿圆锥的侧面爬行一周再回到A,则蚂蚁行迹的最短路程是( )
如图,课桌上放着一个圆锥SO,点A为圆锥底面圆周上一点,SA=2cm,OA=1cm,蚂蚁从点A沿圆锥的侧面爬行一周再回到A,则蚂蚁行迹的最短路程是( )| A. | 2πcm | B. | 2$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com