
分析 使用余弦定理解出.
解答 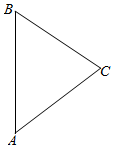 解设两船从A地出发,40分钟后分别到达B地,C地.
解设两船从A地出发,40分钟后分别到达B地,C地.
由题意知∠A=45°,AB=10×$\frac{2}{3}$=$\frac{20}{3}$km,AC=7×$\frac{2}{3}$=$\frac{14}{3}$km.
在△ABC中,由余弦定理得BC2=AB2+AC2-2AB×AC×cosA=$\frac{596-280\sqrt{2}}{9}$.
∴BC=$\frac{2\sqrt{149-70\sqrt{2}}}{3}$.
答:经过40min,两艇相距$\frac{2\sqrt{149-70\sqrt{2}}}{3}$千米.
点评 本题考查了解三角形的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
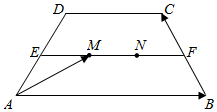 如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.
如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com