考点:数列与函数的综合,等比关系的确定
专题:函数的性质及应用,等差数列与等比数列,不等式
分析:(Ⅰ)令x
1=x
2=
.根据f(x
1+x
2)=1+f(x
1)+f(x
2).得到f(
)+1=
[f(
)+1],求出f(
)+1=1,问题得以证明,
(Ⅱ)由(Ⅰ)求得f(n)=2n-1,再利用放缩法,求得T
2n-T
n>
>
,n≥2,n∈N
*,再由题意log
2(x+1)<
,解得x的即可
解答:
解:(Ⅰ)令x
1=x
2=
.
则f(
+
)=f(
)=1+f(
)+f(
)=1+2f(
),
∴f(
)+1=2[f(
)+1],
∴f(
)+1=
[f(
)+1],
令x
1=x
2=
,
则f(1)=1+2f(
).
∵函数f(x)过定点(1,1),
∴f(1)=1,
∴f(
)=0,
∴f(
)+1=1,
∴数列{f(
)+1}(n∈N
*)是以1为首项,以
为公比的等比数列.
(Ⅱ)由(Ⅰ)知f(
)+1=
()n-1,
即f(
)=
()n-1-1,
令x=
,
∴f(x)=2x-1,
∴f(n)=2n-1,
∴b
n=
=
,
∴T
n=1+
+
+…+
,T
2n=1+
+
+…+
+
+
+…+
,
∴T
2n-T
n=
+
+…+
>
+
+…+
=
>
,
∵不等式T
2n-T
n>
log
2(x+1)(n≥2,n∈N
*)恒成立
∴
>
log
2(x+1)恒成立,
即log
2(x+1)<
=log
2,
∴0<x+1<
,
解得-1<x<
故实数x的取值范围为(-1,
)
点评:本题考查了数列和函数的关系,以及等比数列的定义通项问题,以及利用放缩法证明不等式恒成立的问题,考查了学生的对知识的运用能力,计算能力,转化能力,本题综合性强,属于难题



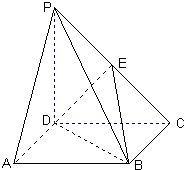 如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.