
分析 本题考查的知识点是归纳推理,我们可以根据已知条件中的等式,分析等式两边的系数及指数部分与式子编号之间的关系,易得等式右边展开式中的第三项分别为:1,3,6,10,…,归纳后即可推断出a2的等式.
解答 解:由已知中的式了,我们观察后分析:
等式右边展开式中的第三项分别为:1,3,6,10,…,
即:1,1+2.1+2+3,1+2+3+4,…
根据已知可以推断:
第n(n∈N*)个等式中a2为:1+2+3+4+…+n=$\frac{n(n+1)}{2}$.
故答案为:$\frac{n(n+1)}{2}$.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
已知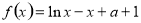 .
.
(1)若存在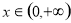 使得
使得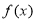 ≥0成立,求
≥0成立,求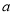 的范围;
的范围;
(2)求证:当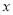 >1时,在(1)的条件下,
>1时,在(1)的条件下,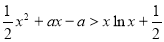 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|-1≤x≤1} | C. | {x|x<-1或x>1} | D. | {x|x≤-1或x≥1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
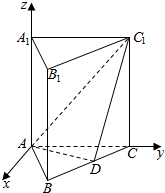 已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).
已知正三棱柱ABC-A1B1C1的各棱长均为1,D是BC上一点,AD⊥C1D,以A为坐标原点,平面ABC内AC的垂线,AC,AA1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则点D的坐标为($\frac{\sqrt{3}}{4}$,$\frac{3}{4}$,0),平面ADC1的一个法向量为($\sqrt{3}$,-1,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com