考点:多面体和旋转体表面上的最短距离问题
专题:计算题,空间位置关系与距离
分析:连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B,从而PN=PH.(实现了转化,这步是解题之关键),最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH,即可得出结论.
解答:
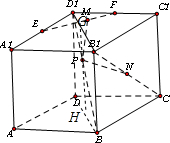
解:首先PM的最小值就是P到EF的距离.
连接B
1D
1交EF于G,连接PG,则EF⊥平面B
1D
1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D
1G为D
1B
1的四分之一.其次,连接BD,设其中点为H,连接PH,BC
1,则△D
1DB≌△D
1C
1B,从而PN=PH.(实现了转化,这步是解题之关键)
最后,连接GH交BD
1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH.
∵正方体ABCD-A
1B
1C
1D
1的棱长为1,
∴GH=
=
.
故选:B.
点评:本题考查多面体和旋转体表面上的最短距离问题,考查学生分析解决问题的能力,有难度.

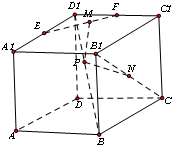
 解:首先PM的最小值就是P到EF的距离.
解:首先PM的最小值就是P到EF的距离. 

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案