
分析 根据二项式定理计算a,再根据定积分的几何意义和性质计算即可.
解答 解:∵${(\frac{a}{{\sqrt{x}}}-x)^6}$展开式的常数项为15,∴C${\;}_{6}^{2}$($\frac{a}{\sqrt{x}}$)4x2=15,
∴a4=1,又a>0,∴a=1.
∵y=$\sqrt{1-{x}^{2}}$表示半径为1的上半圆,y=sin2x是奇函数,
∴${∫}_{-1}^{1}\sqrt{1-{x}^{2}}dx$=$\frac{π}{2}$,${∫}_{-1}^{1}sin2xdx$=0,
∴$\int_{-a}^a{(\sqrt{1-{x^2}}+sin2x)dx}$=$\frac{π}{2}+0$=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查了二项式定理,定积分的计算,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=tan({2x+\frac{π}{6}})$ | B. | $y=cot({x-\frac{π}{6}})$ | C. | $y=tan({2x-\frac{π}{6}})$ | D. | y=tan2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{24}{29}$ | C. | $\frac{16}{31}$ | D. | $\frac{16}{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
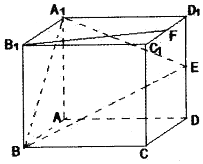 如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E、F分别是棱DD1、C1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
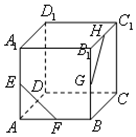 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com