
分析 利用条件,弦化切,再代入计算,即可得出结论.
解答 解:∵$\frac{sinθ-cosθ}{sinθ+cosθ}$=$\frac{1}{2}$,
∴2sinθ-2cosθ=sinθ+cosθ,
∴sinθ=3cosθ,
∴tanθ=3.
(1)3cos2θ-sin2θ+1=4cos2θ-2sinθcosθ+sin2θ=$\frac{4co{s}^{2}θ-2sinθcosθ+s{in}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$=$\frac{4-2tanθ+ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{4-2×3+9}{1+9}$=$\frac{7}{10}$;
(2)$\frac{1-2co{s}^{2}\frac{θ}{2}+2sinθ}{2sin(θ+\frac{3π}{4})}$=$\frac{-cosθ+2sinθ}{-\sqrt{2}sinθ+\sqrt{2}cosθ}$=$\frac{-1+2tanθ}{-\sqrt{2}tanθ+\sqrt{2}}$=$\frac{5}{-2\sqrt{2}}$=-$\frac{5\sqrt{2}}{4}$.
点评 本题考查三角函数值的计算,考查学生的计算能力,正确弦化切是关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
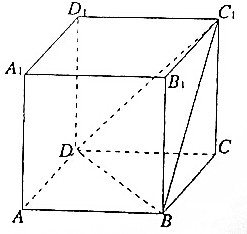 如图所示,已知棱长为1的正方体ABCD-A1B1C1D1,
如图所示,已知棱长为1的正方体ABCD-A1B1C1D1,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com