
分析 由余弦定理求得cosA,可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=4×4×$\frac{7}{8}$=14,再由内角平分线定理,可得AD=$\frac{2}{3}$$\overrightarrow{AC}$,再由向量的加减运算和数量积的性质:向量的平方即为模的平方,计算即可得到所求值.
解答 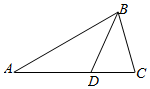 解:由余弦定理可得cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$
解:由余弦定理可得cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$
=$\frac{16+16-4}{2×4×4}$=$\frac{7}{8}$,
可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=4×4×$\frac{7}{8}$=14,
由BD为∠ABC的平分线,可得
$\frac{AD}{CD}$=$\frac{AB}{CB}$=$\frac{4}{2}$=2,
AD=$\frac{2}{3}$$\overrightarrow{AC}$,
即有$\overrightarrow{AC}$•$\overrightarrow{BD}$=$\overrightarrow{AC}$•($\overrightarrow{AD}$-$\overrightarrow{AB}$)=$\overrightarrow{AC}$•($\frac{2}{3}$$\overrightarrow{AC}$-$\overrightarrow{AB}$)
=$\frac{2}{3}$$\overrightarrow{AC}$2-$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{2}{3}$×16-14=-$\frac{10}{3}$.
故答案为:-$\frac{10}{3}$.
点评 本题考查向量的加减运算和数量积的定义及性质,考查向量的平方即为模的平方,以及内角平分线定理的运用,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1(x<0) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1(x>0) | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=0(x<0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 身高x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 63 | 66 | 70 | 72 | 74 |
| A. | 70.12kg | B. | 70.29kg | C. | 70.55kg | D. | 71.05kg |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac2>bc2 | B. | a2>b2 | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | a3>b3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{7}$,0) | B. | (0,-$\sqrt{7}$) | C. | (-5,0) | D. | (-4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{81}{10}$] | B. | (0,$\frac{101}{10}$] | C. | (0,+∞) | D. | (2,$\frac{81}{10}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | -1 | 0 | 1 |
| P | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
| A. | 3 | B. | 1 | C. | 0 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com