Question

9．已知A，B分别为椭圆$\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1（a＞b＞0）的右顶点和上顶点，直线y=kx（k＞0）与椭圆交于C，D两点，若四边形ABCD的面积最大值为2c²，则椭圆的离心率为（　　）

• A． $\frac{1}{3}$
• B． $\frac{1}{2}$
• C． $\frac{\sqrt{3}}{3}$
• D． $\frac{\sqrt{2}}{2}$

Answer 1

分析 联立直线方程和椭圆方程，求出C，D的坐标，得到|CD|，再由点到直线的距离公式求出A，B到直线的距离，把四边形的面积转化为两个三角形的面积和，由基本不等式求得最大值，结合最大值为2c²求得椭圆的离心率．

解答 解：如图，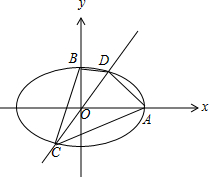

联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$，得C（$-\frac{ab}{\sqrt{{a}^{2}{k}^{2}+{b}^{2}}}，-\frac{kab}{\sqrt{{a}^{2}{k}^{2}+{b}^{2}}}$），D（$\frac{ab}{\sqrt{{a}^{2}{k}^{2}+{b}^{2}}}，\frac{kab}{\sqrt{{a}^{2}{k}^{2}+{b}^{2}}}$），
∴|CD|=$\sqrt{\frac{4{a}^{2}{b}^{2}}{{a}^{2}{k}^{2}+{b}^{2}}+\frac{4{k}^{2}{a}^{2}{b}^{2}}{{a}^{2}{k}^{2}+{b}^{2}}}$=$2ab•\sqrt{\frac{1+{k}^{2}}{{a}^{2}{k}^{2}+{b}^{2}}}$．
A（a，0）到直线kx-y=0的距离为${d}_{1}=\frac{|ak|}{\sqrt{{k}^{2}+1}}$=$\frac{ak}{\sqrt{{k}^{2}+1}}$，
B（0，b）到直线kx-y=0的距离为${d}_{2}=\frac{|-b|}{\sqrt{{k}^{2}+1}}=\frac{b}{\sqrt{{k}^{2}+1}}$，
∴四边形ABCD的面积S=$\frac{1}{2}•2ab•\sqrt{\frac{1+{k}^{2}}{{a}^{2}{k}^{2}+{b}^{2}}}•\frac{ak+b}{\sqrt{{k}^{2}+1}}$=$ab•\sqrt{\frac{（ak+b）^{2}}{{a}^{2}{k}^{2}+{b}^{2}}}$=$ab•\sqrt{1+\frac{2akb}{{a}^{2}{k}^{2}+{b}^{2}}}≤\sqrt{2}ab$．
当且仅当ak=b，即k=$\frac{b}{a}$时上式等号成立，
∴$\sqrt{2}ab=2{c}^{2}$，即2a²b²=4c⁴，∴a²b²=2c⁴，
则a²（a²-c²）=2c⁴，解得：$e=\frac{\sqrt{2}}{2}$．
故选：D．

点评 本题考查了椭圆的几何性质，训练了点到直线的距离公式的应用，考查了利用基本不等式求最值，是中档题．