
| A. | $\frac{2π}{3}$ | B. | $-\frac{2}{3}π$ | C. | $-\frac{π}{3}$ | D. | $-\frac{π}{6}$ |
分析 首先求得f'(x)=$\frac{1}{1+cosx}$,然后根据f'(x0)=2进行解答.
解答 解:由$f(x)=\frac{sinx}{1+cosx}$,得:
f'(x)=$\frac{(sinx)′(1+cosx)-sinx(1+cosx)′}{(1+cosx)^{2}}$
=$\frac{cosx+co{s}^{2}x+si{n}^{2}x}{(1+cosx)^{2}}$=$\frac{1+cosx}{(1+cosx)^{2}}$=$\frac{1}{1+cosx}$.
所以f'(x0)=$\frac{1}{1+cos{x}_{0}}$=2,
所以cosx0=-$\frac{1}{2}$,
因为x∈(-π,0).
所以x=-$\frac{2}{3}$π.
故选B.
点评 本题主要考察了同角三角函数关系式,考查计算能力,属于基础题型.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1,y=x0 | B. | $y=x\;,\;y=\root{3}{x^3}$ | ||
| C. | $y=\sqrt{x-1}•\sqrt{x+1}\;,\;y=\sqrt{{x^2}-1}$ | D. | $y=|x|\;,\;y={(\sqrt{x})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | [$\frac{13}{4}$,2) | C. | [$\frac{13}{8}$,2) | D. | (-∞,$\frac{13}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
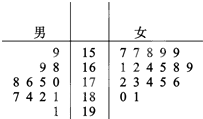 某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm
某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com