
【题目】已知函数 ![]() .
.
(1)求函数 ![]() 的最大值;
的最大值;
(2)设 ![]() ,且
,且 ![]() ,证明:
,证明: ![]() .
.
【答案】(1)0;(2)见解析
【解析】
(1)由题意,求得函数的导数![]() ,利用导数得到函数的单调性,即可求解最大值。
,利用导数得到函数的单调性,即可求解最大值。
(2)由(1),把当-1<x<0时,g(x)<1等价于设f(x)>x,构造新函数h(x)=f(x)-x,利用导数得到函数的单调性和极值,即可求解。
(1)由题意,求得![]() .
.
当x∈(-∞,0)时,![]() >0,f(x)单调递增;
>0,f(x)单调递增;
当x∈(0,+∞)时,![]() <0,f(x)单调递减.
<0,f(x)单调递减.
所以f(x)的最大值为f(0)=0.
(2)由(1)知,当x>0时,f(x)<0,g(x)<0<1.
当-1<x<0时,g(x)<1等价于设f(x)>x.
设h(x)=f(x)-x,则![]() .
.
当x∈(-1,-0)时,0<-x<1,0<![]() <1,则0<
<1,则0<![]() <1,
<1,
从而当x∈(-1,0)时,![]() <0,h(x)在(-1,0)单调递减.
<0,h(x)在(-1,0)单调递减.
当-1<x<0时,h(x)>h(0)=0,即g(x)<1.综上,总有g(x)<1.


科目:高中数学 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(1)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(2)若甲必选![]() ,记
,记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,D为AC的中点.
,D为AC的中点.
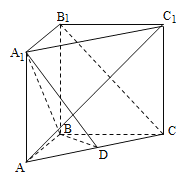
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)设E是![]() 上一点,试确定E的位置使平面
上一点,试确定E的位置使平面![]() 平面BDE,并说明理由.
平面BDE,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国有多个地方盛产板栗,但板栗的销售受季节的影响,储存时间不能太长.某校数学兴趣小组对近几年某食品销售公司的板栗销售量y(吨)和板栗的销售单价x(元/千克)之间的关系进行了调查,得到下表数据:
销售单价x(元/千克) | 11 | 10.5 | 10 | 9.5 | 9 | 8 |
销售量y(吨) | 5 | 6 | 8 | 10 | 11 | 14.1 |
(1)根据前5组数据,求出y关于x的线性回归方程;
(2)若线性回归方程得到的估计数据与剩下的检验数据的误差不超过0.5,则认为线性回归方程是理想的,试问(1)中得到的线性回归方程是否理想?
(附:线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,且
两点,且![]() ,抛物线的准线
,抛物线的准线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 于点
于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,且
两点,且![]() ,点
,点![]() 为线段
为线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点,则点
轴的交点,则点![]() 的横坐标
的横坐标![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com