
分析 (1)利用点与函数的关系,推出递推关系式,然后求解通项公式.
(2)化简数列的通项公式,利用错位相减法求和即可.
解答 解:(1)由题可得${S_n}=\frac{1}{4}{a_n}^2+\frac{1}{2}{a_n}-\frac{15}{4}$
当n≥2时,${S_{n-1}}=\frac{1}{4}{a_{n-1}}^2+\frac{1}{2}{a_{n-1}}-\frac{15}{4}$
所以${a_n}=\frac{1}{4}{a_n}^2+\frac{1}{2}{a_n}-\frac{1}{4}{a_{n-1}}^2-\frac{1}{2}{a_{n-1}}$…(2分)
所以${a_n}^2-2{a_n}-{a_{n-1}}^2-2{a_{n-1}}=0$
所以(an+an-1)(an-an-1-2)=0
因为an>0
所以an-an-1=2…(4分)
当n=1时,${S_1}=\frac{1}{4}{a_1}^2+\frac{1}{2}{a_1}-\frac{15}{4}$,所以${a_1}^2-2{a_1}-15=0$
因为a1>0,所以a1=5…(5分)
所以数列{an}是以5为首项,2为公差的等差数列.
所以an=5+2(n-1)=2n+3…(6分)
(2)由(1)可得${b_n}=({2n+3})•{3^n}$…(7分)
${T_n}=5×3+7×{3^2}+9×{3^3}+…+({2n+3})•{3^n}$
$3{T_n}=5×{3^2}+7×{3^3}+9×{3^4}+…+({2n+3})•{3^{n+1}}$…(8分)
所以$-2{T_n}=5×3+2×{3^2}+2×{3^3}+2×{3^4}+…+2×{3^n}-({2n+3})•{3^{n+1}}$
=$15+2×\frac{{9({1-{3^{n-1}}})}}{1-3}-({2n+3})•{3^{n+1}}$…(10分)
=6-(2n+2)•3n+1 …(11分)
所以${T_n}=({n+1})•{3^{n+1}}-3$…(12分)
点评 本题考查数列与函数相结合,递推关系式以及数列求和的方法,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
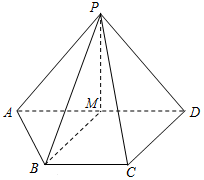 如图,在四棱锥P-ABCD中,M为AD的中点.
如图,在四棱锥P-ABCD中,M为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{4}$,$\frac{π}{3}$) | B. | ($\frac{π}{3}$,$\frac{2π}{3}$) | C. | ($\frac{2π}{3}$,$\frac{5π}{6}$) | D. | (0,$\frac{π}{3}$)∪($\frac{3π}{4}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{15}$ | B. | $\frac{3}{5}$ | C. | $\frac{11}{15}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com