
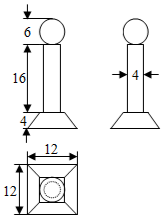
 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.分析 根据三视图知几何体是一个组合体:上面是球、中间是圆柱、下面是正四棱台,并对应的数据,
(Ⅰ)根据球体、柱体和台体的体积公式分别计算,再求和即可;
(Ⅱ)由条件先求出正四棱台的斜高,由梯形的面积公式求出奖杯底座的侧面积.
解答 解:根据三视图知几何体是一个组合体:上面是球、中间是圆柱、下面是正四棱台,
球的半径是3;圆柱的底面半径是2、母线长是16;
正四棱台上底、下底分别为6、12,高为4,
(Ⅰ)球的体积V球=$\frac{4}{3}π{r}^{3}$=$\frac{4}{3}×π×{3}^{3}$=36π(cm3);
圆柱的体积V圆柱=π×22×16=64π(cm3);
V正四棱台=$\frac{1}{3}$×(${6}^{2}+1{2}^{2}+\sqrt{{6}^{2}×1{2}^{2}}$)×4=336(cm3),
所以此奖杯的体积是V=100π+336≈650(cm3);
(Ⅱ)底座是正四棱台,它的斜高是$\sqrt{(6-3)^{2}+{4}^{2}}$=5(cm),
这个奖杯底座的侧面积S=$\frac{1}{2}×(6+12)×5×4$=180(cm2).
点评 本题考查了由三视图求几何体的体积和表面积,考查空间想象能力、运算能力,三视图正确复原几何体是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ex(cosx+sinx) | B. | ex(cosx-sinx) | C. | -ex(cosx+sinx) | D. | ex(sinx-cosx) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{11\sqrt{2}}}{15}$ | B. | $-\frac{{9\sqrt{2}}}{5}$ | C. | $\frac{{9\sqrt{2}}}{5}$ | D. | $\frac{{11\sqrt{2}}}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin4x | B. | y=cos22x-sin22x | C. | y=tan2x | D. | y=cos2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com