
分析 本题可利用AB中点M去研究,先通过坐标关系,将$|\overrightarrow{OA}+\overrightarrow{OB}|$转化为$\overrightarrow{OM}$,用根据AB=2$\sqrt{3}$,得到M点的轨迹,由图形的几何特征,求出$\overrightarrow{OM}$模的最小值,得到本题答案.
解答 解:设A(x1,y1),B(x2,y2),AB中点M(x′,y′).
∵x′=$\frac{{x}_{1}+{x}_{2}}{2}$,y′=$\frac{{y}_{1}+{y}_{2}}{2}$,
∴$\overrightarrow{OA}+\overrightarrow{OB}$=(x1+x2,y1+y2)=2$\overrightarrow{OM}$,
∵圆C:x2+y2-6x+5=0,
∴(x-3)2+y2=4,圆心C(3,0),半径CA=2.
∵点A,B在圆C上,AB=2$\sqrt{3}$,
∴CA2-CM2=($\frac{1}{2}$AB)2,
即CM=1.
点M在以C为圆心,半径r=1的圆上.
∴OM≥OC-r=3-1=2.
∴|$\overrightarrow{OM}$|≥2,∴$|\overrightarrow{OA}+\overrightarrow{OB}|$≥4,
∴$|\overrightarrow{OA}+\overrightarrow{OB}|$的最小值为4.
故答案为:4.
点评 本题考查了数形结合思想和函数方程的思想,可利用AB中点M去研究,先通过坐标关系,将本题考查了数形结合思想和函数方程的思想,可利用AB中点M去研究,先通过坐标关系,得到M点的轨迹,由图形的几何特征,求出结果.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
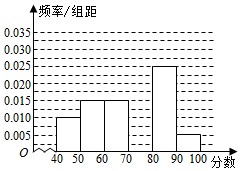 某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的部分频率分布直方图.在统计方法中,同一组数据常用该组区间的中点值作为代表,观察图形的信息,据此估计本次考试的平均分为71.
某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的部分频率分布直方图.在统计方法中,同一组数据常用该组区间的中点值作为代表,观察图形的信息,据此估计本次考试的平均分为71.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com