
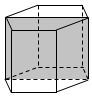
 如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )
如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )| A. | $\frac{{3\sqrt{3}}}{4}$m3 | B. | $\frac{3}{4}$m3 | C. | 1m3 | D. | $\frac{1}{2}$m3 |
分析 根据正六边形的性质求出底面边长,利用矩形的面积得出棱柱的高.
解答 解:设正六棱柱的底面边长为a,高为h,
则$\left\{\begin{array}{l}{2ah=1}\\{\sqrt{3}a=1}\end{array}\right.$,解得a=$\frac{\sqrt{3}}{3}$,h=$\frac{\sqrt{3}}{2}$.
∴六棱柱的体积V=$\frac{\sqrt{3}}{4}×(\frac{\sqrt{3}}{3})^{2}×6×\frac{\sqrt{3}}{2}$=$\frac{3}{4}$.
故选B.
点评 本题考查了正棱柱的结构特征,棱柱的体积计算,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=sinx在第三象限内是增函数 | B. | 函数y=sinx(x∈R)的值域是(-1,1) | ||
| C. | y=cosx在x=2kπ(k∈Z)时取值最大 | D. | y=tanx在整个定义域内都是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉R,x2≠x | B. | ?x∈R,x2=x | C. | ?x0∈R,x${\;}_{0}^{2}$≠x0 | D. | ?x0∈R,x${\;}_{0}^{2}$=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 公差为5的等差数列 | B. | 公差为6的等差数列 | ||
| C. | 公比为6的等比数列 | D. | 公比为8的等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{5}$i | C. | -$\frac{3}{5}$ | D. | -$\frac{3}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
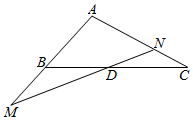 如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )
如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com