
分析 (1)由题意$\frac{c}{a}=\frac{1}{2}$,a-c=1,解出a,c及b的值即可;
(2)先讨论当k不存在时,$\overrightarrow{OA}•\overrightarrow{OB}$的值,当当k存在时,可设直线方程为y=kx+2,联立方程组,由△>0求出k的范围,由根与系数关系用k表示x1+x2,x1x2,由向量的坐标运算用k表示$\overrightarrow{OA}•\overrightarrow{OB}$,即可求出$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围.
解答 解:(1)由题意得$\frac{c}{a}=\frac{1}{2}$,即a=2c,且a-c=1,
∴a=2,c=1,
故b2=a2-c2=3,
∴椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)①当k不存在时,$A(0,-\sqrt{3})$,$B(0,\sqrt{3})$,
∴$\overrightarrow{OA}•\overrightarrow{OB}=(0,-\sqrt{3})•(0,\sqrt{3})=-3$;
②当k存在时,设直线方程为y=kx+2,则有$\left\{\begin{array}{l}y=kx+2\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,整理得(3+4k2)x2+16kx+4=0,
∴${x_1}+{x_2}=-\frac{16k}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{4}{{3+4{k^2}}}$,(i)
又$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}={x_1}{x_2}+(k{x_1}+2)(k{x_2}+2)$,
=(1+k2)x1x2+2k(x1+x2)+4,
=$1+\frac{1}{{3+4{k^2}}}-\frac{{32{k^2}+24-24}}{{3+4{k^2}}}+4$,
=$-3+\frac{25}{{3+4{k^2}}}$,(ii)
△=256k2-16(4k2+3)>0,从而${k^2}>\frac{1}{4}$,(iii)
(iii)代入(ii)中$\overrightarrow{OA}•\overrightarrow{OB}≤-3+\frac{25}{3+1}=\frac{13}{4}$,
∴$\overrightarrow{OA}•\overrightarrow{OB}∈(-∞,\frac{13}{4}]$.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,向量数量积的坐标运算,圆锥曲线与函数的单调性与最值得关系,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
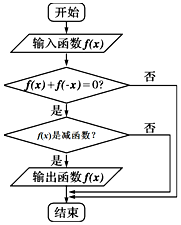 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=lg$\frac{1-x}{1+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-2\sqrt{2},2\sqrt{2}}]$ | B. | [-4,4] | C. | [-5,5] | D. | $[{-5\sqrt{2},5\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{12π}$ | B. | $\frac{25}{24π}$ | C. | $\frac{3+\sqrt{3}}{2π}$ | D. | $\frac{3+\sqrt{3}}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e) | B. | (-∞,-1) | C. | (1,+∞) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com