
分析 (1)可设出直线的方程令y=0和x=0求出A和B两点坐标,然后表示出面积的关系式,求出面积最小时k的值,然后代入得到直线l的方程即可;
(2)|MA|•|MB|=$\sqrt{\frac{1}{{k}^{2}}+1}•\sqrt{4+4{k}^{2}}$=$\frac{2(1+{k}^{2})}{|k|}$=2[-$\frac{1}{k}$+(-k)],利用基本不等式,即可得出结论.
解答 解:设直线l:y-1=k(x-2)(k<0),则有A(2-$\frac{1}{k}$,0)、B(0,1-2k).
(1)由三角形面积S=$\frac{1}{2}$(1-2k)(2-$\frac{1}{k}$),得4k2+2(S-2)k+1=0.
因为△=4(S-2)2-16≥0,
所以S≥4或S≤0(舍去).
又当S≥4时,k<0,
所以△AOB面积的最小值为4.
此时,由4k2+4k+1=0,得k=-$\frac{1}{2}$.
所以直线方程为y-1=-$\frac{1}{2}$(x-2),即x+2y-4=0.
(2)因为|MA|•|MB|=$\sqrt{\frac{1}{{k}^{2}}+1}•\sqrt{4+4{k}^{2}}$=$\frac{2(1+{k}^{2})}{|k|}$=2[-$\frac{1}{k}$+(-k)]≥4(因为k<0),
当且仅当-k=-$\frac{1}{k}$,即k=-1时,|MA|•|MB|取最小值4.此时直线方程为x+y-3=0.
点评 考查学生会求直线与x轴、y轴的截距,会利用基本不等式求面积的最小值,会写出直线的一般式方程.


科目:高中数学 来源: 题型:解答题
| X | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
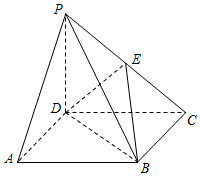 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com