
几何证明选讲.
如图,直线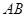 过圆心
过圆心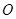 ,交⊙
,交⊙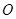 于
于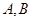 ,直线
,直线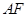 交⊙
交⊙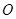 于
于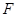 (不与
(不与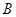 重合),直线
重合),直线 与⊙
与⊙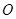 相切于
相切于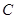 ,交
,交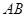 于
于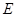 ,且与
,且与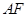 垂直,垂足为
垂直,垂足为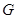 ,连结
,连结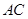 .
.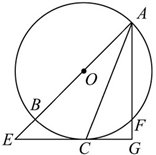
求证:(1)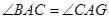 ;
;
(2)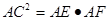 .
.
(1)连结BC,得∠ACB=∠AGC=90°.根据GC切⊙O于C,∴∠GCA=∠ABC.∴∠BAC=∠CAG.
(2)连结CF,证得△ACF∽△AEC. 推出AC2=AE·AF.
解析试题分析:(1)连结BC,∵AB是直径,∴∠ACB=90°,∴∠ACB=∠AGC=90°.
∵GC切⊙O于C,∴∠GCA=∠ABC.∴∠BAC=∠CAG. 5分
(2)连结CF,∵EC切⊙O于C, ∴∠ACE=∠AFC. 又∠BAC=∠CAG,
∴△ACF∽△AEC. ∴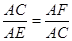 ,∴AC2=AE·AF. 10分
,∴AC2=AE·AF. 10分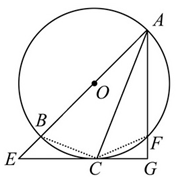
考点:圆,弦切角定理,相似三角形。
点评:中档题,涉及平面几何选讲,难点往往不大,注意考查圆与三角形的基本性质及相关结论,注意充分考察图形的几何特征,探寻解题途径。


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com