
 已知全集U=R,集合A={x|x(x+2)<0},B={x||x|≤1},则如图阴影部分表示的集合是( )
已知全集U=R,集合A={x|x(x+2)<0},B={x||x|≤1},则如图阴影部分表示的集合是( )| A. | (-2,1) | B. | [-1,0]∪[1,2) | C. | (-2,-1)∪[0,1] | D. | [0,1] |
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:选择题
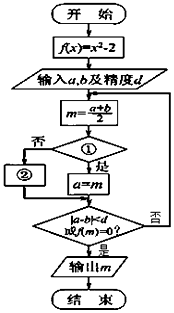
| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
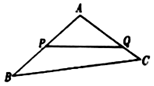 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
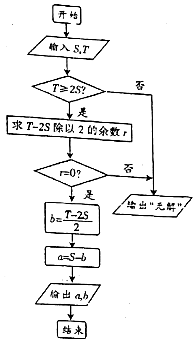
| A. | 17,23 | B. | 21,21 | C. | 19,23 | D. | 20,20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{4}+\frac{3}{4}i$ | B. | $\frac{1}{4}-\frac{3}{4}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com