Question

11．已知△ABC的三边长分别为AB=5，BC=4，AC=3，M是AB边上的点，P是平面ABC外一点，给出下列四个命题：
①若PA⊥平面ABC，则三棱锥P-ABC的四个面都是直角三角形；
②若PM⊥平面ABC，且M是AB边的中点，则有PA=PB=PC；
③若PC=5，PC⊥平面ABC，则△PCM面积的最小值为$\frac{15}{2}$；
④若PB=5，PB⊥平面ABC，则三棱锥P-ABC的外接球体积为$\frac{{125\sqrt{2}π}}{3}$；
其中正确命题的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 ①根据空间中的垂直关系，能得出三棱锥P-ABC的四个面都是直角三角形；
②根据空间中的垂直关系与三角形全等，得出PA=PB=PC；
③根据图形求出△PCM面积的最小值为6，不是$\frac{15}{2}$；
④利用直三棱锥P-ABC的外接球是以AC、BC、PB为棱长的长方体的外接球，
求出它的体积即可．

解答 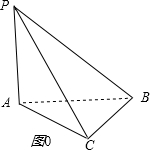解：对于①，如图0所示，
PA⊥平面ABC，
AC?平面ABC，∴PA⊥AC，∴△PAC是直角三角形；
同理，△PAB是直角三角形，
又△ABC的三边长分别为AB=5，BC=4，AC=3，
∴AB²=AC²+BC²，
∴AC⊥BC，△ABC是直角三角形；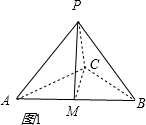
又PA⊥BC，PA∩AC=A，
∴BC⊥平面PAC，
∴BC⊥PC，∴△PBC是直角三角形；
即三棱锥P-ABC的四个面都是直角三角形，①正确；
对于②，如图1所示，
∵△ABC是直角三角形，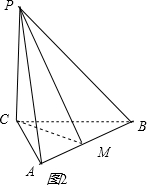
且M是AB的中点，
∴MA=MB=MC；
又PM丄平面ABC，
∴Rt△PMA≌Rt△PMB≌Rt△PMC，
∴PA=PB=PC，②正确；
对于③，如图2所示，
当PC⊥面ABC时，
∴△PCM的面积为$\frac{1}{2}$×PC×CM=$\frac{1}{2}$×5×CM
又∵CM作为垂线段时最短．为$\frac{3×4}{5}$=$\frac{12}{5}$，
∴△PCM面积的最小值为$\frac{1}{2}$×5×$\frac{12}{5}$=6，③不正确；
对于④，如图3所示，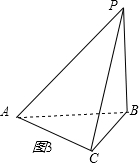
当PB=5，PB⊥平面ABC时，AB=5，BC=4，AC=3，
∴直三棱锥P-ABC的外接球可以看做是
AC=3，BC=4，PB=5为棱长的长方体的外接球，
∴2R=PA=5$\sqrt{2}$，
∴R=$\frac{5\sqrt{2}}{2}$，
其体积为$\frac{4π}{3}$•${（\frac{5\sqrt{2}}{2}）}^{3}$=$\frac{125\sqrt{2}π}{3}$，④正确．
综上，正确的命题为①②④．
故选：C．

点评 本题考查了空间中的平行与垂直关系的应用问题，也考查了空间中的角与距离的计算问题，是综合性题目．