
分析 (1)计算a1=0,故a1•a2•a3=0;
(2)根据对数性质得出an=1•0+2•1+22•2+23•3+…+2n-1•(n-1),使用错位相减法求出an,得出a的值.
解答 解:(I)a1=[log21]=0,a2=[log21]+[log22]+[log23]=0+1+1=2,
a3=[log21]+[log22]+[log23]+…+[log27]=0+1+1+2+2+2+2=10.
∴a1•a2•a3=0.
(II)当2n-1≤x≤2n-1时,[log2x]=n-1.
∴[log22n-1]+[log22n-1+1]+[log22n-1+2]+…+[log2(2n-1)]=(n-1)(2n-1-2n-1+1)=2n-1(n-1).
∴an=1•0+2•1+22•2+23•3+…+2n-1•(n-1),①
∴2an=22•1+23•2+24•3+…+2n•(n-1),②
②-①得:an=-22-23-24-…-2n-1+2n•(n-1)-2
=-$\frac{{2}^{2}(1-{2}^{n-2})}{1-2}$+2n•(n-1)-2
=2n•(n-2)+2.
又an=(n-2)•2n+a,
∴a=2.
点评 本题考查了对数的运算性质,数列求和的应用,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
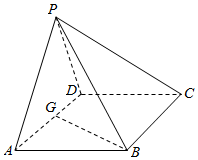 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin3>sin2 | B. | cos3>cos2 | C. | cos(-$\frac{2}{5}$π)<cos(-$\frac{1}{4}$π) | D. | sin$\frac{12}{5}$π<sin$\frac{17}{4}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y大大增大,x一定变大,z可能不变 | B. | y大大增大,x可能不变,z变大 | ||
| C. | y大大增大,x可能不变,z也不变 | D. | y可能不变,x可能不变,z可能不变 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com