
分析 由已知可得An$(\frac{n}{n+1},\frac{n+1}{n})$,Bn$(\frac{n+1}{n},\frac{n}{n+1})$,则线段AnBn的垂直平分线为y=x.可得线段AnM的垂直平分线为:$y-\frac{2n+1}{2n}$=$\frac{n}{n+1}(x-\frac{2n+1}{2n+2})$,把y=x代入解得xn.再利用“裂项求和”即可得出.
解答 解:由已知可得An$(\frac{n}{n+1},\frac{n+1}{n})$,Bn$(\frac{n+1}{n},\frac{n}{n+1})$,则线段AnBn的垂直平分线为y=x.
线段AnM的垂直平分线为:$y-\frac{2n+1}{2n}$=$\frac{n}{n+1}(x-\frac{2n+1}{2n+2})$,
把y=x代入解得xn=2+$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+1})$.
∴{xn}的前n项和Tn=2n+$\frac{1}{2}[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$=2n+$\frac{1}{2}(1-\frac{1}{n+1})$=2n+$\frac{n}{2n+2}$=$\frac{4{n}^{2}+5n}{2n+2}$.
故答案为:$\frac{4{n}^{2}+5n}{2n+2}$.
点评 本题考查了线段的垂直平分线及其性质、三角形的外心、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
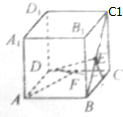 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 随$|\overrightarrow a|$增大而增大 | B. | 随$|\overrightarrow a|$增大而减小 | C. | 是2 | D. | 是4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com