
| A. | $\frac{\sqrt{3}π}{12}$ | B. | $\frac{\sqrt{3}π}{24}$ | C. | 1-$\frac{\sqrt{3}π}{12}$ | D. | 1-$\frac{\sqrt{3}π}{24}$ |
分析 根据题意,记“蚂蚁距三角形三个顶点的距离均超过1”为事件A,则其对立事件B为“蚂蚁与三角形的三个顶点的距离不超过1”,先求得边长为4的等边三角形的面积,再计算事件B构成的区域面积,由几何概型可得P(B),进而由对立事件的概率性质,可得答案.
解答 解:记“蚂蚁距三角形三个顶点的距离均超过1”为事件A,则其对立事件B为“蚂蚁与三角形的三个顶点的距离不超过1”,
边长为4的等边三角形的面积为S=$\frac{\sqrt{3}}{4}$×42=4$\sqrt{3}$,
则事件B构成的区域面积为S(B)=3×$\frac{π}{3}×\frac{1}{2π}$×π×12=$\frac{π}{2}$,
由几何概型的概率公式得P(B)=$\frac{\sqrt{3}π}{24}$,
P(A)=1-P(,B)=1-$\frac{\sqrt{3}π}{24}$,
故选:D.
点评 本题考查几何概型,涉及对立事件的概率性质;解题时如需要计算不规则图形的面积,可用间接法.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
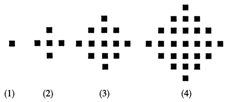 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2017 | B. | 4034 | C. | 2016 | D. | 4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 101 | B. | 808 | C. | 1212 | D. | 2012 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c,d中至少有一个正数 | B. | a,b,c,d全为正数 | ||
| C. | a,b,c,d全都大于或等于0 | D. | a,b,c,d中至多有一个负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 买票→候车厅候车→上车→候车检票口检票 | |
| B. | 候车厅候车→买票→上车→候车检票口检票 | |
| C. | 买票→候车厅候车→候车检票口检票→上车 | |
| D. | 候车厅候车→上车→候车检票口检票→买票 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com