
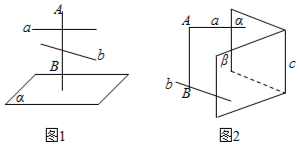
分析 (1)在α内构造分别于a,b平行的直线a',b',只需证明a',b'是相交直线即可;
(2)设b与β的交点为N,过B作α的垂线BM,利用线面垂直的性质即可得出a∥BM,故而AB⊥平面BMN,由线面垂直的性质可得c⊥b,c⊥BM,故而c⊥平面BMN,于是c∥AB.
解答 证明:(1)∵a∥α,b∥α,
∴存在a'?α,b'?α,使得a∥a',b∥b'.
∵若a'∥b',则a∥b,与a、b为异面直线相矛盾,
∴a',b'为相交直线.
∵AB⊥a,AB⊥b,
∴AB⊥a',AB⊥b'.
∴AB⊥α.
(2)设b与平面β的垂足为N,过B作BM⊥α,垂足为M,
∵a⊥α,BM⊥α,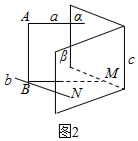
∴a∥BM,∵AB⊥a,
∴AB⊥BM,又∵AB⊥b,b∩BM=B,
∴AB⊥平面BMN.
∵BM⊥α,b⊥β,α∩β=c,
∴BM⊥c,b⊥c,又b∩BM=B,
∴c⊥平面BMN,
∴AB∥c.
点评 本题考查了线面平行的性质与判定,构造直线是解决问题的关键之处.


科目:高中数学 来源: 题型:选择题
 把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C,(其中BD=2AD,BC=AC)则异面直线DC,AB所成角的正切值为( )
把一副三角板ABC与ABD摆成如图所示的直二面角D-AB-C,(其中BD=2AD,BC=AC)则异面直线DC,AB所成角的正切值为( )| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $\frac{{\sqrt{21}}}{7}$ | D. | $\frac{{\sqrt{21}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
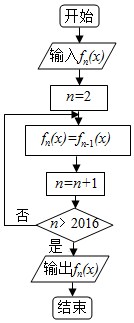 如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )| A. | $\sqrt{2}sin(x+\frac{π}{4})$ | B. | $-\sqrt{2}sin(x+\frac{π}{4})$ | C. | $\sqrt{2}sin(x-\frac{π}{4})$ | D. | $-\sqrt{2}sin(x-\frac{π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=-$\frac{4}{3}$,b=$\frac{1}{3}$ | B. | k=-$\frac{4}{3}$,b=-$\frac{1}{3}$ | C. | k=$\frac{4}{3}$,b=$\frac{1}{3}$ | D. | k=$\frac{4}{3}$,b=-$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com