
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 2.5 | 3 | 4 | 4.5 | 5.22 | 5.97 |
���� ��1�����ݱ���ֱ����x��y��ƽ���������ϵ��$\widehat{b}$��$\widehat{a}$��ֵ������ع鷽�̼��ɣ�
��2���ֱ�x=7��8���뷽���������жϼ��ɣ�
��3����x��ֵ�������ʽ���㼴�ɣ�
��� �⣺��1��$\overline{x}$=4.5��$\overline{y}$=3.5
$\stackrel{��}{b}$=$\frac{3.5}{5}$=0.7��$\widehat{a}$=0.35��
����$\stackrel{��}{y}$=0.7x+0.35��
��2���ɣ�1����֪��
��x=7ʱ��y=5.25��5.25-5.22=0.03��0.05
��x=8ʱ��y=5.95��5.97-5.95=0.02��0.05
���ԣ��˻ع�ֱ�߷���������
��3���ɣ�1����֪����x=100ʱ��y=70.35���֣�
���ԣ�������90-70.35=19.65�֣�
���� ���⿼���˻ع鷽�������Լ��ع鷽�̵�Ӧ�ã����������������һ���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 14 | B�� | 8 | C�� | 6 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=8 | B�� | x=-8 | C�� | x=-16 | D�� | x=16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x+$\frac{1}{x}$ | B�� | y=sin��+$\frac{1}{sin��}$��0���ȣ�$\frac{��}{2}$�� | ||
| C�� | y=sin��+$\frac{1}{sin��}$��0���ȣ��У� | D�� | $\frac{1}{{\sqrt{{x^2}+2}}}+\sqrt{{x^2}+2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����P-ABCD�ĵ���ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��BD=$2\sqrt{2}$��������P-BC-D����ֵ�Ĵ�С��
��ͼ����P-ABCD�ĵ���ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��BD=$2\sqrt{2}$��������P-BC-D����ֵ�Ĵ�С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{4\sqrt{3}}}{3}$ | B�� | $2\sqrt{3}$ | C�� | 6 | D�� | $4\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡЭ��У��������һ��ѧ���ģ��Ծ��������棩 ���ͣ������
��֪���� ��
��
��1���� ������
������ �ļ�ֵ�͵������䣻
�ļ�ֵ�͵������䣻
��2���������� �����ٴ���һ��
�����ٴ���һ�� ��ʹ��
��ʹ��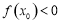 ��������ʵ��
��������ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com