
| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
分析 本题为几何概型,由题意通过圆和三角形的知识画出满足条件的图形,分别找出满足条件的点集对应的图形面积,及图形的总面积,作比值即
解答 解:以AB为直径圆内的区域为满足∠AMB>90°的区域, 则P落在半圆内,
则P落在半圆内,
半圆的面积为$\frac{1}{2}$π×42=8π;
正方形ABCD的面积为64.
∴满足∠AMB>90°的概率为$\frac{{S}_{半圆}}{{S}_{正方形}}$=$\frac{8π}{64}=\frac{π}{8}$;
故选:A.
点评 本题考查几何概型;几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式解答.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-2} | B. | {x|x<2} | C. | {x|-2<x<2} | D. | {x|x>-2,x≠1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{1}{2}$x+$\frac{π}{6}}$),x∈R | B. | y=sin($\frac{1}{2}$x+$\frac{π}{12}$),x∈R | ||
| C. | y=sin(2x+$\frac{π}{3}$),x∈R | D. | y=sin(2x+$\frac{π}{6}$),x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
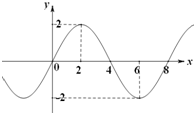 函数f(x)=Asin(ωx+ϕ)(其中A>0,ω>0)的部分图象如图所示,则f(2)+f(3)+…+f(2016)的值为( )
函数f(x)=Asin(ωx+ϕ)(其中A>0,ω>0)的部分图象如图所示,则f(2)+f(3)+…+f(2016)的值为( )| A. | $\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | 0 | D. | $-\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com