练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．设函数f（x）=（$\frac{1}{2}$）10-ax，其中a为常数，且f（3）=$\frac{1}{16}$．
    （1）求a的值；
    （2）若f（x）≥4，求x的取值范围．

    分析 （1）根据f（3）=$\frac{1}{16}$，求出a的值即可；（2）根据指数函数的性质求出x的范围即可．

    解答 解：（1）函数f（x）=（$\frac{1}{2}$）10-ax，
    由f（3）=$\frac{1}{16}$，得：${（\frac{1}{2}）}^{10-3a}$=$\frac{1}{16}$，
    得：3a-10=-4，解得：a=2；
    （2）由（1）f（x）=22x-10，
    由f（x）≥4，得：22x-10≥22，
    故2x-10≥2，解得：x≥6．

    点评 本题考查了指数函数的性质，考查求函数的解析式以及解不等式问题，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知某批零件的长度误差（单位：毫米）服从正态分布N（0，22），从中随机取一件，其长度误差落在区间（2，4）内的概率为（　　）（若随机变量ξ服从正态分布N（μ，σ2），则P（μ-σ＜ξ＜μ+σ）=68.26%，P（μ-2σ＜ξ＜μ+2σ）=95.44%）
    A．4.56%B．13.59%C．27.18%D．31.74%

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知三条不重合的直线m，n，l和两个不重合的平面α，β，下列命题正确的是（　　）
    A．若m∥n，n?α，则m∥αB．若l∥n，m⊥n，则l∥m
    C．若l⊥α，m⊥β，且l⊥m，则α⊥βD．若α⊥β，α∩β=m，且m⊥n，则n⊥α

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

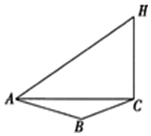    13．某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性，特对其进行了一项测试．如图，这种烟花在燃放点C进行燃放实验，测试人员甲、乙分别在A，B两地（假设三地在同一水平面上），测试人员甲测得A、B两地相距80米且∠BAC=60°，甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒．在A地测得该烟花升至最高点H处的仰角为60°．（已知声音的传播速度为340米∕秒）
    （1）求甲距燃放点C的距离；
    （2）求这种烟花的垂直“冲天”高度HC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．在△ABC中，点D满足$\overrightarrow{BC}$=3$\overrightarrow{BD}$，则（　　）
    A．$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$B．$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$C．$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$D．$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．设数列{an}满足a1=$\frac{1}{3}$，an+1=an+$\frac{{{a}_{n}}^{2}}{{n}^{2}}$，n∈N*，证明：
    （1）数列{an}为递增数列；
    （2）$\frac{n}{2n+1}$≤an≤$\frac{2n-1}{2n+1}$，n∈N*．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=ax+lnx，x∈（1，e）．
    （1）当a=-$\frac{1}{2}$时，求f（x）的单调区间；
    （2）若f（x）有极值，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若变量x，y满足约束条件$\left\{\begin{array}{l}x≥1\\ y≤2\\ x-y≤1\end{array}\right.$，则z=2x-y的最大值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数$f（x）=\frac{x}{4}+\frac{a}{x}-lnx$，其中a∈R，且曲线y=f（x）在点（1，f（1））处的切线垂直于直线$y=\frac{1}{2}x$
    （1）求实数a的值
    （2）求函数f（x）的单调区间．

    查看答案和解析>>

    同步练习册答案