考点:命题的真假判断与应用
专题:圆锥曲线的定义、性质与方程
分析:①设A、B为两个定点,k为非零常数,
||-||=k,利用双曲线定义可知:只有当k<|AB|时,动点P的轨迹为双曲线;
②垂直于同一直线的两条直线可能相互平行、相交或为异面直线;
③向量
=(1,2)按
=(1,1)平移得到的仍然是向量
;
④双曲线
-=1与椭圆
+y2=1有相同的焦点
(±,0);
⑤把(-x,-y)代入曲线x
3-y
3+9x
2y+9xy
2=0得到曲线的方程没有变化,可得:此曲线的图象关于原点对称.
解答:
解:①设A、B为两个定点,k为非零常数,
||-||=k,只有当k<|AB|时,动点P的轨迹为双曲线,因此不正确;
②垂直于同一直线的两条直线相互平行、相交或为异面直线,因此不正确;
③向量
=(1,2)按
=(1,1)平移得到的仍然是向量
,而不是
=(2,3),因此不正确;
④双曲线
-=1与椭圆
+y2=1有相同的焦点
(±,0),正确;
⑤把(-x,-y)代入曲线x
3-y
3+9x
2y+9xy
2=0得到-x
3+y
3-9x
2y-9xy
2=0,化为x
3-y
3+9x
2y+9xy
2=0,因此曲线的方程没有变化,可得:此曲线的图象关于原点对称.因此正确.
综上可知:只有④⑤正确.
故答案为:④⑤.
点评:本题综合考查了圆锥曲线的定义标准方程及其性质、空间中线线位置关系、曲线的对称性等基础知识与基本技能方法,考查了推理能力,属于难题.



 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.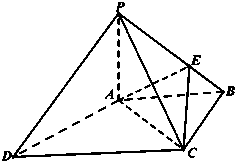 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.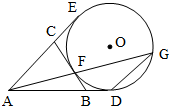 如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是
如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是