
 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.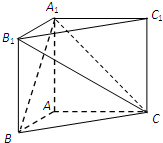
| 2 |
| 2 |
| 1+a2 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 进入2013年后全国各地雾霾天气频发,一个重要的诱因是空气中细小颗粒物.我国新引入PM2.5来衡量大气的质量.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.长沙市环保局从该市市区2013年1月份的PM2.5监测数据中随机抽取7天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
进入2013年后全国各地雾霾天气频发,一个重要的诱因是空气中细小颗粒物.我国新引入PM2.5来衡量大气的质量.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.长沙市环保局从该市市区2013年1月份的PM2.5监测数据中随机抽取7天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).查看答案和解析>>
科目:高中数学 来源: 题型:
| PA |
| PB |
| a |
| b |
| c |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(4,+∞) |
| B、(-∞,-4) |
| C、(-∞,-4] |
| D、[-4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com