
| t | 50 | 110 | 250 |
| Q | 150 | 108 | 150 |
分析 (1)根据数据选择合适的函数类型,利用待定系数法进行求解.
(2)结合一元二次函数的性质求解即可.
解答 解:(1)由数据可知,刻画芦荟种植成本Q与上市时间t的变化关系的函数不可能是常值函数,
若用函数Q=at+b,Q=a•bt,Q=alogbt中的任意一个来反映时都应有a≠0,
且上述三个函数均为单调函数,这与表格所提供的数据不符合,…(2分)
所以应选用二次函数Q=at2+bt+c进行描述.…(3分)
将表格所提供的三组数据分别代入函数Q=at2+bt+c,可得:
$\left\{\begin{array}{l}{150=2500a+50b+c}\\{108=12100a+110b+c}\\{150=62500a+250b+c}\end{array}\right.$,
解得a=$\frac{1}{200}$,b=-$\frac{3}{2}$,c=$\frac{425}{2}$.…(9分)
所以,刻画芦荟种植成本Q与上市时间t的变化关系的函数为Q=$\frac{1}{200}$t2-$\frac{3}{2}$t+$\frac{425}{2}$.…(10分)
(2)当t=-$\frac{-\frac{3}{2}}{2×\frac{1}{200}}$=150(天)时,…(12分)
芦荟种植成本最低为Q=$\frac{1}{200}$×1502-$\frac{3}{2}$×150+$\frac{425}{2}$=100(元/10 kg).…(14分)
点评 本题主要考查函数模型的应用,考查学生的运算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
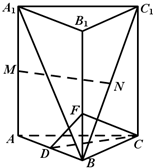 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 科目 | 基本素质 | 专业技能 | 计算机 | 礼仪 |
| 合格的概率 | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|x<-1} | D. | {x|x>0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com