
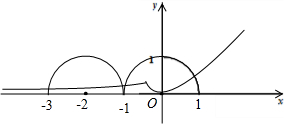
 若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为
若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为| x | (-∞,-1) | -1 | (-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
| 1 |
| e |
| 1 |
| e |


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com