Question

20．已知F为抛物线C：y²=5x的焦点，点A（3，1），M是抛物线C上的动点，当|MA|+|MF|取最小值$\frac{17}{4}$时，
点M的坐标为（$\frac{1}{5}$，1）．

Answer 1

分析 根据抛物线的定义，将|MA|+|MF|转化成|MA|+|PM|．由平面几何知识，可得当P、A、M三点共线时，|MA|+|PM|有最小值．由此即可得到|MA|+|MF|取最小值，进而得到相应的点M的坐标．

解答 解：由题意y²=5x得 F（$\frac{5}{4}$，0），准线方程为 x=-$\frac{5}{4}$，点A（3，1），P（-$\frac{5}{4}$，1）
设点M到准线的距离为d=|PM|，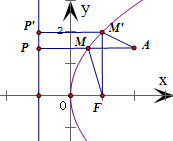
则由抛物线的定义得|MA|+|MF|=|MA|+|PM|，
故当P、A、M三点共线时，|MF|+|MA|取得最小值为|AP|=3-（-$\frac{5}{4}$）=$\frac{17}{4}$，
再将y=1代入抛物线y²=5x 得 x=$\frac{1}{5}$，故点M的坐标是：（$\frac{1}{5}$，1）．
故答案为：$\frac{17}{4}$，（$\frac{1}{5}$，1）

点评 本题考查抛物线的定义和性质得应用，考查运算求解能力，考查数形结合思想，解答的关键利用是抛物线定义，体现了转化的数学思想．