
| A. | $\frac{1}{7}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
分析 由题意,线段PF1的垂直平分线恰过点F2,垂直为D,则yA=$\frac{1}{4}$yp,根据三角形的面积公式计算即可.
解答 解:由题意,线段PF1的垂直平分线恰过点F2,垂直为D,则yD=2yA=$\frac{1}{2}$yp,yA=$\frac{1}{4}$yp,
∴$\frac{{S}_{△O{F}_{1}A}}{{S}_{△P{F}_{1}{F}_{2}}}$=$\frac{\frac{1}{2}c•{y}_{A}}{\frac{1}{2}•2c•{y}_{D}}$=$\frac{1}{8}$,
故选:D.
点评 本题考查了双曲线的简单性质和三角形的面积公式,属于基础题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
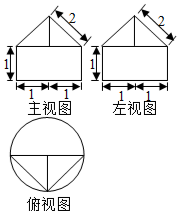 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 2π+$\frac{\sqrt{3}}{3}$ | B. | π+$\frac{\sqrt{3}}{3}$ | C. | 2π+$\frac{\sqrt{3}}{3}$ | D. | π+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩 编号 | 1 | 2 | 3 | 4 | 5 |
| 物理(x) | 90 | 85 | 74 | 68 | 63 |
| 数学(y) | 130 | 125 | 110 | 95 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=P | B. | P≠M | C. | N∩P≠∅ | D. | M∩N≠∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{15}{2}$ | B. | -2 | C. | $\frac{15}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com