
| A. | (-∞,-$\frac{1}{4}$]∪[$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{1}{4}$]∪[$\frac{1}{4}$,+∞)∪{0} | C. | $[{-\frac{1}{4},0})∪({0,\frac{1}{4}}]$ | D. | $[{-\frac{1}{4},\frac{1}{4}}]$ |
分析 利用圆的对称性,通过x的范围,利用基本不等式求解表达式的范围,判断即可.
解答 解:圆x2+(y-2)2=1的圆心(0,2),半径为:1;可知x∈[-1,1],
当x>0时y>0,则0<$\frac{xy}{{4{x^2}+{y^2}}}$=$\frac{1}{4\frac{x}{y}+\frac{y}{x}}$≤$\frac{1}{2\sqrt{\frac{4x}{y}•\frac{y}{x}}}$=$\frac{1}{4}$当且仅当y=2x=$\frac{6}{5}$时取等号.
由圆的对称性可知:x<0时,则$\frac{xy}{{4{x^2}+{y^2}}}$∈[-$\frac{1}{4}$,0)
当x=0时,则$\frac{xy}{{4{x^2}+{y^2}}}$=0,则$\frac{xy}{{4{x^2}+{y^2}}}$的取值范围是[-$\frac{1}{4}$,$\frac{1}{4}$]
故选:D.
点评 本题考查直线与圆的位置关系的应用,基本不等式的应用不等式的最值的求法,考查计算能力.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 10 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
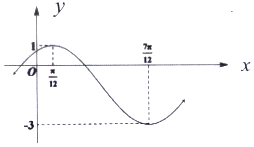 已知函数$f(x)=Asin(wx+φ)(A>0,w>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(wx+φ)(A>0,w>0,|φ|<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-1) | B. | (1,-1) | C. | (-1,1) | D. | (1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com