练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则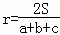，类比这个结论可知：四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4，内切球半径为r，四面体S﹣ABC的体积为V，则r=（　　）

    　

    A．

    B．

    　

    C．

    D．


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


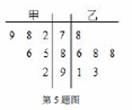
    为了从甲乙两人中选一人参加数学竞赛，老师将二人最近6次数学测试的分数进行统计，甲乙两人的平均成绩分别是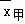、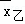，则下列说法正确的是（　　）

    　

    A．

    ＞，乙比甲成绩稳定，应选乙参加比赛

    　

    B．

    ＞，甲比乙成绩稳定，应选甲参加比赛

    　

    C．

    ＜，甲比乙成绩稳定，应选甲参加比赛

    　

    D．

    ＜，乙比甲成绩稳定，应选乙参加比赛

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在空间直角坐标系中，点P在x轴正半轴上，它到Q（0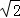，，3）的距离为2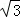，则点P的坐标为（　　）

    　

    A．

    （2，0，0）

    B．

    （﹣1，0，0）

    C．

    （0，0，1）

    D．

    （1，0，0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    关于x的不等式E：ax2+ax﹣2≤0，其中a∈R．

    （Ⅰ）若a=1时，求不等式E的解集；

    （Ⅱ）若不等式E在R上恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知p：x=2，q：0＜x＜3，则p是q的（　　）

    　

    A．

    充分不必要条件

    B．

    必要不充分条件

    　

    C．

    充要条件

    D．

    既不充分，又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图，AC为⊙O的直径，OB⊥AC，弦BN交AC于点M．若OC=，OM=1，则MN=　_________　．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


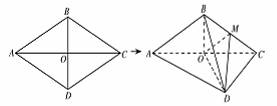
    如图，菱形ABCD的边长为4，∠BAD=60°，AC∩BD=O．将菱形ABCD沿对角线AC折起，得到三棱锥B﹣ACD，点M是棱BC的中点，DM=2．

    （1）求证：OM∥平面ABD；

    （2）求证：平面DOM⊥平面ABC；

    （3）求三棱锥B﹣DOM的体积．

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


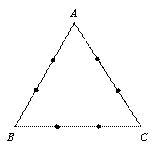
    如图所示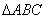，是边长为3的正三角形，若在每一边的两个三等分点中，各随机选取一点连成三角形，下列命题正确的是（写出所有正确命题的编号）： 

    ①依此方法可能连成的三角形一共有8个；

    ②这些可能连成的三角形中，恰有3个是直角三角形；

    ③这些可能连成的三角形中，恰有2个是锐角三角形；

    ④这些可能连成的三角形中，恰有2个是钝角三角形.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    班级53名同学报名参加科技、文化、生活三个学习社团，规定每人必须参加一个社团，且最多参加两个社团，在所有可能的报名方案中，设参加社团完全相同的人数的最大值为n，则n的最小值为　_________　．

    查看答案和解析>>

    同步练习册答案