考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知得2b
n=a
n+a
n+1,
an+12=bnbn+1,进一步得
an+1=,联立后可得{
}是等差数列,由等差数列的通项公式求数列{
}的通项公式,进一步求得{b
n}的通项公式,结合
an=求得数列{a
n}的通项公式;
(2)由(1)得
=,然后利用裂项相消法求得S
n,代入不等式
2aSn<2-化为
4a(-)<2-,然后转化为关于n的函数分类求解实数a的取值范围.
解答:
(1)证明:由已知,得2b
n=a
n+a
n+1 ①,
an+12=bnbn+1 ②,
由②可得
an+1= ③,
将③代入①,得对任意n≥2,n∈N
*,有
2bn=+,即
2=+,
∴{
}是等差数列.
设数列{
}的公差为d,由a
1=10,a
2=15,得
b1=,b
2=18,
∴
=,
=3,
d=-=,
∴
=+(n-1)d=+(n-1)=
(n+4),
bn=.
由已知,当n≥2时,
an==,而a
1=10也满足此式.
∴数列{a
n}、{b
n}的通项公式为:
an=,
bn=.
(2)解:由(1),得
==
2(-),
则
Sn=2[(-)+(-)+…+(-)]=2(-)=
2(-),
不等式
2aSn<2-化为
4a(-)<2-,
不等式化为(a-1)n
2+(3a-6)n-8<0,
设f(n)=(a-1)n
2+(3a-6)n-8,则f(n)<0对任意n∈N
*恒成立.
当a-1>0,即a>1时,不满足条件.
当a-1=0,即a=1时,满足条件.
当a-1<0,即a<1时,函数f(n)图象的对称轴为直线
x=-<0,f(n)关于n递减,
只需f(1)=4a-15<0,解得
a<,故a<1.
综上可得,a的取值范围是(-∞,1].
点评:本题考查了等差数列和等比数列的性质,考查了裂项相消法求数列的前n项和,考查了数学转化、分类讨论等数学思想方法,考查了数列的函数特性,是中档题.



 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案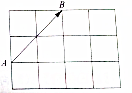 如图所示是4×3的矩形(每个小方格都是单位正方形),在起点和中点都在小方格的顶点处的向量中,试问:
如图所示是4×3的矩形(每个小方格都是单位正方形),在起点和中点都在小方格的顶点处的向量中,试问: