17．若方程${2}^{7{x}^{2}-13x-m}$=（$\frac{1}{2}$）^-mx-2的一个根在区间（0，1）内，另一个根在区间（1，2）内，则实数m的取值范围是（-4，-2）．

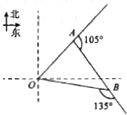16．如图，一只蜘蛛从点O出发沿北偏东45°方向爬行xcm，到达点A处捕捉到一只小虫，然后沿OA方向右转105°爬行10cm，到达点B处捕捉哦另一只小虫，这时他沿AB方向右转135°爬行回到它的出发点O处，那么x=$\frac{10\sqrt{6}}{3}$．

15．已知半径为3的扇形的弧长为4π，则这个扇形的圆心角的弧度数为$\frac{4π}{3}$．

14．已知一个扇形的半径为4cm，圆心角为60°，则扇形的弧长为$\frac{4π}{3}$cm．

13．变量x与变量y有如下对应关系

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

则其线性回归直线必过定点（4，5）．

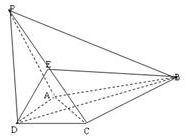12．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AD⊥CD，且DB平分∠ADC，E为PC的中点，AD=CD=1，DB=2$\sqrt{2}$，PD=2．
 （1）证明：PA∥平面BDE；
（2）证明：AC⊥PB；
（3）求三棱锥E-ABD的体积．

11．已知点A（3，4）和B（0，8），则|AB|=（　　）

A．

25

B．

5

C．

$\sqrt{7}$

D．

7

10．某研究机构对高三学生的记忆力x和判断力y进行统计分析，所得数据如表所示：

x	6	8	10	12
y	2	3	5	6

（1）在给定的坐标系中画出表中数据的散点图；
（2）试根据最小二乘法原理，求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并在给定的坐标系中画出回归直线；
（3）试根据（2）求出的线性回归方程，预测记忆力为9的学生的判断力．
参考公式：用最小二乘法求线性回归方程系数公式：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}，\hat a=\overline y-\hat b\overline x$．

9．生物兴趣小组的同学到野外调查某种植物的生长情况，共测量了k∈Z株该植物的高度（单位：厘米），获得数据如下：
6，7，8，9，10，14，16，17，17，18，19，20，20，21，24，26，26，27，28，29，29，30，30，30，31，31，33，36，37，41．
根据上述数据得到样本的频率分布表如下：

分组	频数	频率
[5，15]	6	0.2
（15，25]	9	0.3
（25，35]	n1	f1
（35，45]	n2	f2

（1）确定样本频率分布表中n₁，n₂，f₁和f₂的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）用（2）的频率分布直方图估计该植物生长高度的平均值．

8．已知盒子中有5个白球、3个黑球，这些球除颜色外完全相同，若从盒子中随机地取出2个球，则其中至少有1个黑球的概率是$\frac{9}{14}$．