
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
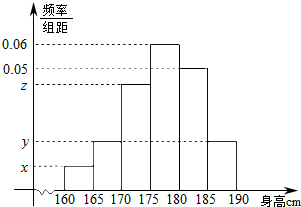 从某学校的800名男生中抽 取40名测量身高,并制成如下频率分布直方图,已知x:y:z=1:2:4.
从某学校的800名男生中抽 取40名测量身高,并制成如下频率分布直方图,已知x:y:z=1:2:4.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{π}{2}$.
如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{π}{2}$.查看答案和解析>>
科目: 来源: 题型:解答题
| 一车间 | 二车间 | 三车间 | |
| 男职工 | 200 | 100 | 250 |
| 女职工 | 600 | k | 550 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com