
科目: 来源: 题型:
【题目】某市为增强市民的环境保护意识, 面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取![]() 名按年龄分组: 第
名按年龄分组: 第![]() 组
组![]() ,第2 组
,第2 组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,
,得到的频率分布直方图如图所示,
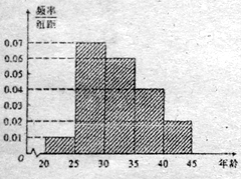
(1)若从第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参与广场的宣传活动, 应从第
名志愿者参与广场的宣传活动, 应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(2)在(1)的条件下, 该县决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验, 求第
名志愿者介绍宣传经验, 求第![]() 组至少有—名志愿者被抽中的概率.
组至少有—名志愿者被抽中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ),且数列
),且数列![]() 是首项为2,公差为2的等差数列.
是首项为2,公差为2的等差数列.
(1)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)设![]() ,如果
,如果![]() 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求函数![]() 在区间
在区间![]() 上的最值;
上的最值;
(Ⅱ)当![]() 时,设函数
时,设函数![]() (其中
(其中![]() 为常数)的3个极值点为
为常数)的3个极值点为![]() ,且
,且![]() ,将
,将![]() 这5个数按照从小到大的顺序排列,并证明你的结论.
这5个数按照从小到大的顺序排列,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ),且数列
),且数列![]() 是首项为2,公差为2的等差数列.
是首项为2,公差为2的等差数列.
(1)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)设![]() ,如果
,如果![]() 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】设有一条光线从![]() 射出,并且经
射出,并且经![]() 轴上一点
轴上一点![]() 反射.
反射.
(1)求入射光线和反射光线所在的直线方程(分别记为![]() );
);
(2)设动直线![]() ,当点
,当点![]() 到
到![]() 的距离最大时,求
的距离最大时,求![]() 所围成的三角形的内切圆(即:圆心在三角形内,并且与三角形的三边相切的圆)的方程.
所围成的三角形的内切圆(即:圆心在三角形内,并且与三角形的三边相切的圆)的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com