
科目: 来源: 题型:
【题目】某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现用分层抽样方法(按
类工人).现用分层抽样方法(按![]() 类,
类,![]() 类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)![]() 类工人和
类工人和![]() 类工人中个抽查多少工人?
类工人中个抽查多少工人?
(2)从![]() 类工人中的抽查结果和从
类工人中的抽查结果和从![]() 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1:

表2:

① 先确定![]() ,
,![]() ,再完成下列频率分布直方图,就生产能力而言,
,再完成下列频率分布直方图,就生产能力而言,![]() 类工人中个体间的差异程度与
类工人中个体间的差异程度与![]() 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
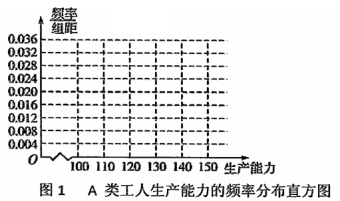
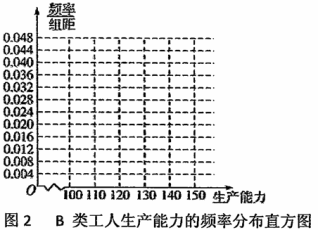
② 分别估计![]() 类工人和
类工人和![]() 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
的数据用该组区间的中点值作代表).
查看答案和解析>>
科目: 来源: 题型:
【题目】未知数的个数多余方程个数的方程(组)叫做不定方程,最早提出不定方程的是我国的《九章算术》.实际生活中有很多不定方程的例子,例如“百鸡问题”:公元五世纪末,我国古代数学家张丘建在《算经》中提出了“百鸡问题”:“鸡母一,值钱三;鸡翁一,值钱二;鸡雏二,值钱一.百钱买百鸡,问鸡翁、母、雏各几何?”
算法设计:
(1)设母鸡、公鸡、小鸡数分别为![]() 、
、![]() 、
、![]() ,则应满足如下条件:
,则应满足如下条件:
![]() ;
;![]() .
.
(2)先分析一下三个变量的可能值.①![]() 的最小值可能为零,若全部钱用来买母鸡,最多只能买33只,
的最小值可能为零,若全部钱用来买母鸡,最多只能买33只,
故![]() 的值为
的值为![]() 中的整数.②
中的整数.②![]() 的最小值为零,最大值为50.③
的最小值为零,最大值为50.③![]() 的最小值为零,最大值为100.
的最小值为零,最大值为100.
(3)对![]() 、
、![]() 、
、![]() 三个未知数来说,
三个未知数来说,![]() 取值范围最少.为提高程序的效率,先考虑对
取值范围最少.为提高程序的效率,先考虑对![]() 的值进行一一列举.
的值进行一一列举.
(4)在固定一个![]() 的值的前提下,再对
的值的前提下,再对![]() 值进行一一列举.
值进行一一列举.
(5)对于每个![]() ,
,![]() ,怎样去寻找满足百年买百鸡条件的
,怎样去寻找满足百年买百鸡条件的![]() .由于
.由于![]() ,
,![]() 值已设定,便可由下式得到:
值已设定,便可由下式得到:![]() .
.
(6)这时的![]() ,
,![]() ,
,![]() 是一组可能解,它只满足“百鸡”条件,还未满足“百钱”.是否真实解,还要看它们是否满足
是一组可能解,它只满足“百鸡”条件,还未满足“百钱”.是否真实解,还要看它们是否满足![]() ,满足即为所求解.
,满足即为所求解.
根据上述算法思想,画出流程图并用伪代码表示.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的曲线.当
(单位:分钟)之间的关系满足如图所示的曲线.当![]() 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当![]() 时,曲线是函数
时,曲线是函数![]() 图象的一部分.根据专家研究,当注意力指数
图象的一部分.根据专家研究,当注意力指数![]() 大于80时学习效果最佳.
大于80时学习效果最佳.
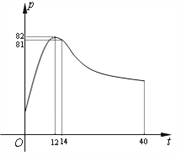
(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴, 建立平面直角坐标系,在平面直角坐标系
轴的正半轴, 建立平面直角坐标系,在平面直角坐标系![]() 中, 直线
中, 直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() .
.
(1)写出曲线![]() 直角坐标方程和直线
直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点, 求
两点, 求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了![]() 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为![]() 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为![]() 元, 求
元, 求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂家计划在2012年举行商品促销活动,经调查测算,该商品的年销售量![]() 万件与年促销费用
万件与年促销费用![]() 万元满足:
万元满足:![]() ,其中
,其中![]() 为常数,若不搞促销活动,则该产品的年销售量只有1万件,已知2012年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).
为常数,若不搞促销活动,则该产品的年销售量只有1万件,已知2012年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).
(1)将2012年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂2012年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目: 来源: 题型:
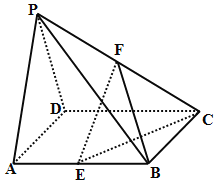
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
(1)求证:EF∥平面PAD;
(2)求三棱锥B-EFC的体积;
(3)求二面角P-EC-D的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com