【题目】个人排成一排，在下列情况下，各有多少种不同排法？

（1）甲不排头，也不排尾，

（2）甲、乙、丙三人必须在一起

（3）甲、乙之间有且只有两人，

在平面直角坐标系中，已知曲线的参数方程为（为参数，）．

（Ⅰ）当时，若曲线上存在两点关于点成中心对称，求直线的参数方程；

（Ⅱ）在以原点为极点，轴的正半轴为极轴的极坐标系中，极坐标方程为的直线与曲线相交于两点，若，求实数的值．

【题目】已知半径为5的圆的圆心在轴上，圆心的横坐标是整数，且与直线相切．

（1）求圆的方程；

（2）设直线与圆相交于、两点，求实数的取值范围；

（3）在（2）的条件下，是否存在实数，使得弦的垂直平分线过点？若存在，求出实数的值；若不存在，请说明理由．

【题目】（本小题满分12分）已知函数，其中，且．

（Ⅰ）讨论函数的单调性；

（Ⅱ）若不等式恒成立，求实数的取值范围．

【题目】已知函数（， ）为奇函数，且相邻两对称轴间的距离为.

（1）当时，求的单调递减区间；

（2）将函数的图象沿轴方向向右平移个单位长度，再把横坐标缩短到原来的（纵坐标不变），得到函数的图象.当时，求函数的值域.

【题目】等比数列{an}中，已知a1=2，a4=16．
（1）求数列{an}的通项公式an；
（2）若a3 ， a5分别是等差数列{bn}的第4项和第16项，求数列{bn}的通项公式及前n项和Sn ．

【题目】某消防机构为四个小区的居民代表进行消防安全知识宣传.在代表中，按分层抽样的方式抽取了10名“幸运之星”，“幸运之星”每人获得一份纪念品.相关数据如下：

(I)求此活动中各小区“幸运之星”的人数；

（II）从B小区和C小区的“幸运之星”中任选两人进行后续的活动，求这两个人均来自B小区的概率；

（III）消防机构在B小区内，对参加问答活动的居民进行了是否有兴趣参加消防安全培训的问卷调查，统计结果如下（单位：人）：

据此判断能否在犯错误的概率不超过的前提下认为有兴趣参加消防安全培训与性别有关系？

临界值表：

参考公式：，其中．

【题目】在如图所示的几何体中，平面平面，四边形是菱形，四边形是矩形，，，，是的中点．

(Ⅰ)求证：平面；

(II)在线段上是否存在一点，使三棱锥的体积为？若存在，求出的长；若不存在，请说明理由．

在平面直角坐标系中，直线的参数方程为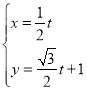（为参数），曲线的普通方程为，以坐标原点为极点，轴的正半轴为极轴建立极坐标系．

（I）求直线的极坐标方程与曲线的参数方程；

（II）设点D在曲线上，且曲线在点D处的切线与直线垂直，试确定点D的坐标.

【题目】在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且 =2csinA
（1）确定角C的大小；
（2）若c= ，且△ABC的面积为 ，求a+b的值．