【题目】已知椭圆： 的短轴长为，右焦点为，点是椭圆上异于左、右顶点的一点．

（1）求椭圆的方程；

（2）若直线与直线交于点，线段的中点为，证明：点关于直线的对称点在直线上．

【题目】在△ABC中，角A、B、C所对的边分别是a、b、c满足：cosAcosC+sinAsinC+cosB= ，且a，b，c成等比数列，
（1）求角B的大小；
（2）若 + = ，a=2，求三角形ABC的面积．

【题目】对于维向量，若对任意均有或，则称为维向量. 对于两个维向量定义.

（1）若, 求的值；

（2）现有一个维向量序列： 若且满足： ，求证：该序列中不存在维向量.

(3) 现有一个维向量序列： 若且满足： ，若存在正整数使得为维向量序列中的项，求出所有的.

【题目】设函数）.

（1）当时，求曲线在点处的切线方程；

（2）设，若对任意的，存在使得成立，求的取值范围.

【题目】已知函数在点处取得极值.

(1)求的值；

(2)若有极大值，求在上的最小值．

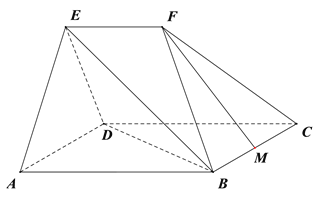
【题目】如图，在几何体中，平面平面，四边形为菱形，且， ， ∥， 为中点．

（Ⅰ）求证： ∥平面；

（Ⅱ）求直线与平面所成角的正弦值；

（Ⅲ）在棱上是否存在点，使 ？ 若存在，求的值；若不存在，说明理由．

【题目】设函数．

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）设，若对任意的，存在使得成立，求的取值范围．

【题目】设数列{an}的前n项和为Sn=2n2 ， {bn}为等比数列，且a1=b1 ， b2（a2﹣a1）=b1 ．
（1）求数列{an}和{bn}的通项公式；
（2）设cn= ，求数列{cn}的前n项和Tn ．

【题目】已知椭圆： 的短轴长为，右焦点为，点是椭圆上异于左、右顶点的一点．

（1）求椭圆的方程；

（2）若直线与直线交于点，线段的中点为，证明：点关于直线的对称点在直线上．